Solving the Maximum Independent Set Problem on QuEra Aquila using the PlanQK Quantum SDK

In this tutorial, you’ll learn how to use the PlanQK Quantum SDK to perform Analog Hamiltonian Simulation on QuEra Aquila. The PlanQK Quantum SDK serves as a wrapper around Braket, offering the same functionality and syntax.

You can use the SDK either directly from your favorite IDE or within a PlanQK service.

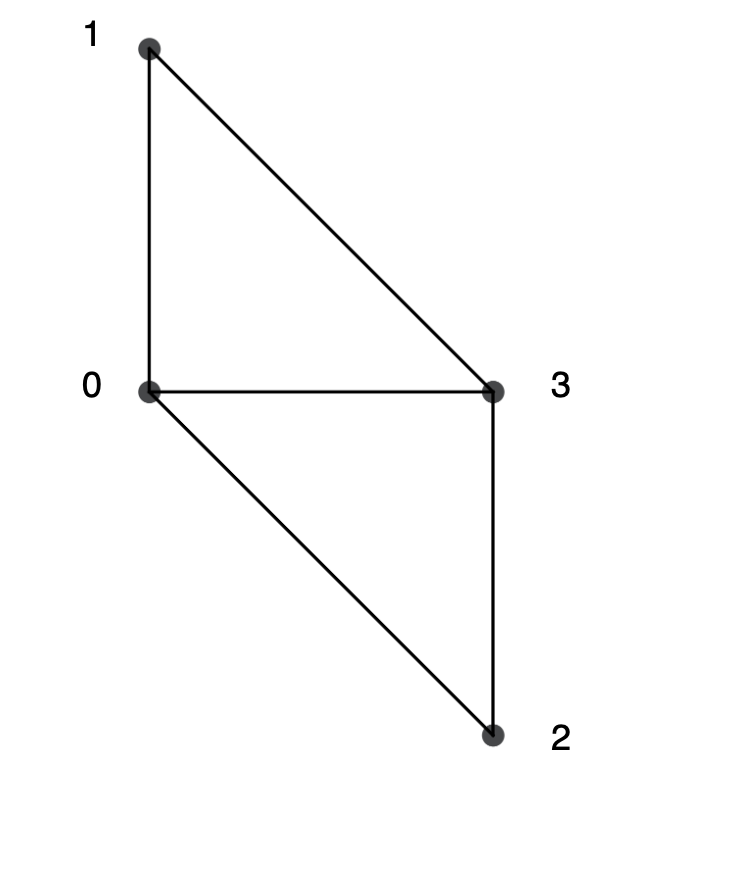
We will explore the Maximum Independent Set (MIS) problem as a practical example. This classic problem in graph theory involves finding the largest subset of nodes in a graph such that no two nodes in the subset are connected by an edge. The MIS problem has wide-ranging applications, including network design, scheduling, and resource allocation.

In the example graph shown to the right, the MIS consists of Node 1 and Node 2. These nodes are not connected to each other, and adding any other node to this subset would create a connection between nodes within the subset, violating the independent set condition.

This tutorial bases on the AWS Braket QuEra tutorials. We recommend reading it for more in-depth information about Analog Hamiltonian Simulation (AHS).

Accessing Aquila with the PlanQK Quantum SDK

To access Aquila with PlanQK SDK you need to have

1. A PlanQK Pro account.
2. The PlanQK Quantum SDK.

Running quantum programs on Aquila incurs execution costs, as detailed on the pricing page. Therefore, you must have a Pro account with a valid credit card linked to it. If you haven't created a PlanQK account yet, you can sign up here.

To upgrade to a Pro account, log in to your Account settings, click on Upgrade, and then select the Subscribe button under the Pro section. Follow the prompts to enter your credit card information.

NOTE

If you are a member of an organization with a Pro account, you do not need to create an individual Pro account.

To install the PlanQK Quantum SDK, ensure you have Python 3.11 or higher installed. The SDK is available on PyPI and can be installed using the following pip command:

pip install planqk-quantum

Implementing the Maximum Independent Set problem with Aquila

To solve an MIS problem using Aquila, one should first understand the nature of the problem and how it will be mapped onto Aquila. As stated above, the MIS problem on a given graph involves finding the largest subset of nodes that are not connected to each other. To encode the MIS problem mathematically, one must minimize a cost function that rewards a high number of nodes while penalizing the inclusion of nodes that are connected.

On Aquila, this problem is natively encodable as you will see below. The qubit encoding in Aquila involves having atoms either in their fundamental ground state or being driven to a highly excited state, called the Rydberg state, through resonant excitations with a laser, referred to here as the driving laser. Entanglement arises when two atoms that are driven to make the transition are close enough to each other: the fact that the Rydberg state is highly excited in the electronic structure of the atom results in an interaction within a given radius, called the Blockade radius, with other atoms. If atoms are within this radius, driving the second atom to the excited state is not possible. This naturally creates the penalty condition of the cost function of the MIS. So if all atoms are driven to make the transition by controlling the parameters of the driving laser, but some are within the blockade radius of each other, this will create an independent set of atoms in the excited state. Then, using adiabatic computation to transition from a simple Hamiltonian to the Hamiltonian encoding the cost function of the MIS problem, one can solve the MIS problem using Aquila.

Creating a program for Aquila to solve the MIS problem

Let’s start by importing the relevant PlanQK and Braket libraries:

from planqk import PlanqkQuantumProvider
from braket.ahs.atom_arrangement import AtomArrangement
from braket.ahs.analog_hamiltonian_simulation import AnalogHamiltonianSimulation
from braket.timings.time_series import TimeSeries
from braket.ahs.driving_field import DrivingField

You can access the Aquila backend via its ID aws.quera.aquila using the PlanqkQuantumProvider object, as shown in the code snippet below. During initialization, you need to provide your access token and optionally your organization ID if you want to access the backend on behalf of your organization.

The access token is required to authenticate your requests to the PlanQK platform and to track the usage costs of your quantum executions. To obtain the token, visit your Platform Home Page and copy it from the Your Personal Access Token section.

provider = PlanqkQuantumProvider(access_token="your-access-token", organization_id="my-org-id")
backend = provider.get_backend("aws.quera.aquila")

Encoding the Graph using Rydberg atoms

Each node in the graph will be represented by an individual Rydberg atom, and the edges will be encoded by positioning connected atoms within the Rydberg blockade radius of each other. The blockade radius is typically a few micrometers, and it determines the distance within which atoms cannot both be excited to Rydberg states simultaneously due to strong interactions.

To systematically arrange the atoms, we’ll place them on a two-dimensional square grid with a spacing of 5.5 micrometers. This grid spacing ensures that atoms representing connected nodes are within each other’s blockade radius, effectively encoding the edges of the graph.

• Edge Encoding: An edge between two nodes (atoms) is represented by placing them either directly adjacent (horizontally or vertically) or diagonally adjacent on the grid.
• Neighbor Distance:
  • Direct Neighbors: For atoms that are horizontally or vertically adjacent, the distance is 5.5 micrometers.
  • Diagonal Neighbors: For atoms that are diagonally adjacent, the distance is \sqrt{2} * 5.5 micrometers, calculated using the Pythagorean theorem.

In Python the arrangement is implemented by the atom_position array. The order of nodes in this array corresponds to their indices in the result bitstring after measurement.

distance = 5.5e-6 # Distance in m 
atom_position = [
    [ 0. , distance],       # Node 0
    [ 0. , 2*distance],     # Node 1
    [ distance,  0. ],      # Node 2
    [ distance,  distance]] # Node 3

Next, add the atom positions to the AtomArrangement object, which will serve as input for the AHS program that will be created later

register = AtomArrangement()
for atom in atom_position:
    register.add(atom)

Driving the Analog Hamiltonian Simulation

Aquila provides three control parameters for the laser that drives the electronic transition: the amplitude (Rabi frequency), the frequency/wavelength (detuning from the resonant frequency), and the phase of the laser relative to the atoms’ position. The initial and final values of the amplitude and detuning must be selected to represent a simple initial Hamiltonian and the final Hamiltonian encoding the MIS problem’s cost function. Typically, for adiabatic computation on Aquila, the initial values are:

• Amp(t=0) = 0
• Detuning(t=0) < 0

And the values at time T, to represent the cost function of the MIS problem, are typically selected as follows::

• Amp(t=T) = 0
• Detuning(t=T) > 0

Generally, during the computation, the amplitude is increased to a certain value and then decreased before reaching its final value.

To control these parameters on Aquila, we need to create a Braket object called TimeSeries, composed of a list of time points, each associated with values of the control parameters. Therefore, let’s first create the time points list, keeping in mind that the maximum duration for a computation on Aquila is 4 microseconds, and the minimum time step is 50 nanoseconds:

time_max = 4e-6 # seconds
tsteps = 5e-8 # seconds
nT=int(time_max/tsteps)+1
time=np.linspace(0, time_max, nT)

Now, let’s create the list of values for the control parameters. Here, we’ll use simple linear ramps without changing the phase, so we’ll create a list of zeros the same length as the time list:

# Create the control functions
amplitude_min = 0       
amplitude_max = 2.5e6 * 2 * np.pi # MHz*2*pi
detuning_min = -9e6 * 2 * np.pi # MHz*2*pi
detuning_max = 7e6 * 2 * np.pi # MHz*2*pi
time_ramp = 0.15*time_max
time_points = [0, time_ramp, time_max - time_ramp, time_max]
amplitude_values = [amplitude_min, amplitude_max, amplitude_max, amplitude_min]
detuning_values = [detuning_min, detuning_min, detuning_max, detuning_max]
phase_values = [0, 0, 0, 0]
amplitude_lin = np.interp(time, time_points, amplitude_values)
detuning_lin = np.interp(time, time_points, detuning_values)
phase_lin = np.interp(time, time_points, phase_values)

Next, let’s associate the list of values and the time points list to create TimeSeries objects:

# Creating the time series from the control functions
amplitude = TimeSeries()
for t_step, val in zip(time, amplitude_lin):
    amplitude.put(t_step, val)
detuning = TimeSeries()
for t_step, val in zip(time, detuning_lin):
    detuning.put(t_step, val)
phase = TimeSeries()
for t_step, val in zip(time, phase_lin):
    phase.put(t_step, val)

We can now create a DrivingField object, which corresponds to the driving part of Aquila’s Hamiltonian:

# Adding the time series to the driving field
drive = DrivingField(
    amplitude=amplitude,
    detuning=detuning,
    phase=phase
)

We can then combine the atomic register created earlier with the DrivingField to create a complete Hamiltonian Simulation program. To ensure compatibility with the QuEra machine, we must round all values to match the precision levels supported by the Aquila QPU:

# Create the AHS program
ahs_program = AnalogHamiltonianSimulation(register=register, hamiltonian=drive)
# Discretize the AHS program according to the device's specifications
discretized_program = ahs_program.discretize(backend)

The discretized program can now be run on Aquila via PlanQK by passing it to the backend’s run function, which returns a Braket task. You can monitor its execution state by calling the state function. After its successful execution, you can retrieve the results:

# Execute the discretized AHS program on the selected backend
task = backend.run(discretized_program)
# Monitor task status and get results
print(f"Task status: {task.state()}")
print(f"Task result: {task.result()}")

Result Interpretation

To process and interpret the results, we need to explain how the measurement of qubit states is performed on Aquila:

Before the time dependent sequence implemented in the AHS (pre-sequence), the atoms are prepared as described above, with all atoms in the fundamental ground state. The atoms at this stage are trapped by laser tweezers that individually keep the atoms in place. An imaging laser is then turned on using fluorescence to make a non-destructive detection of the atoms on the tweezers grid. We can verify if the sequence started with the right register. When the sequence starts, those tweezers are turned off, the computation is performed, and at the end, the trapping lasers are turned back on. The atoms that are still in the ground state are trapped, but the atoms that made the transition to the Rydberg state by the end of the computation are anti-trapped by the tweezers, meaning that because of their state, the tweezers will kick the atoms out of the register. The imaging laser is then turned on using fluorescence to detect the atoms, thus only detecting the atoms that stayed in the ground state. By processing the shot before and after, one can then deduce the state of the qubits:

• Detected in the pre- and post-sequence shot: the atom is in the ground state (here labeled 0).
• Detected in the pre- but not in the post-sequence: the atom is in the excited/Rydberg state (here labeled 1). In our example these are the two atoms representing the MIS nodes 1 and 2.
• Not detected in the pre-sequence: defect in the register creation; this shot should be discarded.

Using this understanding, we can process the measurement data to reconstruct, for each shot, the bitstring representing the qubits’ final states. The following Python code demonstrates how to build a dictionary of counts for each observed bitstring:

result = task.result()

# Extract post-sequence measurements
post_sequences = [list(measurement.post_sequence) for measurement in result.measurements]
post_sequences = ["".join(['1' if site==0 else '0' for site in post_sequence]) for post_sequence in post_sequences]

# Count the occurrences of each bitstring
counters = {}
for post_sequence in post_sequences:
    if post_sequence in counters:
    counters[post_sequence] += 1
    else:
    counters[post_sequence] = 1

The counters dictionary now contains the frequency of each observed bitstring, representing the different possible outcomes of the computation. For instance:

• Based on our atom arrangement a bitstring like '0110', i.e. the solution to our problem, indicates that:
  • The second and the third atoms (MIS nodes 1 and 2) transitioned to the excited state ('1').
  • The first and last two atoms (node 0 and node 3) remained in the ground state ('0').

Full code

from planqk import PlanqkQuantumProvider
from braket.ahs.atom_arrangement import AtomArrangement
from braket.ahs.analog_hamiltonian_simulation import AnalogHamiltonianSimulation
from braket.timings.time_series import TimeSeries
from braket.ahs.driving_field import DrivingField
import numpy as np

# Creates a simple task for Quera solving MIS for the graph given.

# Instantiate the PlanQK provider and select the QuEra Aquila backend
provider = PlanqkQuantumProvider(access_token="your-access-token", organization_id="my-org-id")
backend = provider.get_backend(backend_id="aws.quera.aquila")

# Define a simple atom arrangement
distance = 5.5e-6 # Distance in m 
atom_position = [
    [ 0. , distance],       # Node 0
    [ 0. , 2*distance],     # Node 1
    [ distance,  0. ],      # Node 2
    [ distance,  distance]] # Node 3

# Add the atoms to the register
register = AtomArrangement()
for atom in atom_position:
    register.add(atom)
    
# Create the time points list
time_max = 4e-6 # seconds
tsteps = 5e-8 # seconds
nT=int(time_max/tsteps)+1
time=np.linspace(0, time_max, nT)

# Create the control functions
amplitude_min = 0       
amplitude_max = 2.5e6 * 2 * np.pi # MHz*2*pi
detuning_min = -9e6 * 2 * np.pi # MHz*2*pi
detuning_max = 7e6 * 2 * np.pi # MHz*2*pi
time_ramp = 0.15*time_max
time_points = [0, time_ramp, time_max - time_ramp, time_max]
amplitude_values = [amplitude_min, amplitude_max, amplitude_max, amplitude_min]
detuning_values = [detuning_min, detuning_min, detuning_max, detuning_max]
phase_values = [0, 0, 0, 0]
amplitude_lin = np.interp(time, time_points, amplitude_values)
detuning_lin = np.interp(time, time_points, detuning_values)
phase_lin = np.interp(time, time_points, phase_values)

# Creating the time series from the control functions
amplitude = TimeSeries()
for t_step, val in zip(time, amplitude_lin):
    amplitude.put(t_step, val)
detuning = TimeSeries()
for t_step, val in zip(time, detuning_lin):
    detuning.put(t_step, val)
phase = TimeSeries()
for t_step, val in zip(time, phase_lin):
    phase.put(t_step, val)
    
# Adding the time series to the driving field
drive = DrivingField(
    amplitude=amplitude, 
    detuning=detuning, 
    phase=phase
)

# Create the AHS program
ahs_program = AnalogHamiltonianSimulation(register=register, hamiltonian=drive)

# Discretize the AHS program according to the device's specifications
discretized_program = ahs_program.discretize(backend)

# Execute the discretized AHS program on the selected backend
task = backend.run(discretized_program)

# Get results
result = task.result()
post_sequences = [list(measurement.post_sequence) for measurement in result.measurements]
post_sequences = ["".join(['1' if site==0 else '0' for site in post_sequence]) for post_sequence in post_sequences]
counters = {}
for post_sequence in post_sequences:
    if post_sequence in counters:
        counters[post_sequence] += 1
    else:
        counters[post_sequence] = 1

print(f"Result: {counters}")